ブレーキの鳴き制御解析(複素固有値解析)
ブレーキの鳴き(現象)
ブレーキをかけると、摩擦によって構造の剛性が変化します。さらに、摩擦による損失(減衰)が発生します。その結果、複素固有値の実数成分が正となります。
※ 実数成分=対数増幅で負は減衰、正は自励
ブレーキの鳴きは、低音で150~450Hz、高音で2000Hz以上で発生すると考えられます。人にとってはかなり不快です。
また、鳴き(音)の問題だけでなく、摩擦が発生することによってブレーキの寿命にも影響します。
数学モデル
NX Nastranでモデル化すると以下のようになります。
ここで、\{f\}はブレーキ力\\
\{f\} = ([kbr] + i[kbi]) \{x^*\} \\
よって、 $$ $$[M]\{x^{”}\}+ [C]\{x^{‘}\} + ([K] + ig[K])\{x\} = ([kbr] + i[kbi]) \{x^*\} \tag{2} \\
ここで、 \\
\{x^*\} : ブレーキ力の変位 \\
[kbr] : ブレーキ変位に対する実数剛性(モデルの剛性の変化)\\
[kbi] : ブレーキ変位に対する虚数剛性(モデルの摩擦減衰)\\
$$
式を整理すると、
ブレーキ剛性の取り込み
ブレーキ剛性の取り込みはDMIG(接触初期状態の指定)とK2PP(剛性マトリクスをケースコントロール)を使用します。
DMIGはノード/ノード間への直接マトリクスインプットバルクデータカードを定義します。K2PP=A*DMIGであり、DMIGをモデルに組み込むためのケースコントロールカードを定義します。
メリットとして、サブケース毎にDMIGを切替る ことができ、さらにK2PPを変化させることができるので、ブレーキ力の 変化を考慮した解析ができます。
解析モデル
解析は、下図の簡略化したブレーキモデルに対し、60次までの複素固有値を求めて ブレーキの鳴きが発生するかを確認する。
材料データ
各部位の材料値は下表にまとめます。
| 部位 | 縦弾性率[N/mm^2] | ポアソン比 | 密度[ton/mm^3] | 構造減衰比 |
|---|---|---|---|---|
| ディスク | 21000 | 0.31 | 8E-10 | 0.0015 |
| ハブ | 21000 | 0.31 | 8E-10 | – |
| シュー | 850 | 0.15 | 6.5E-10 | 0.0015 |
複素固有値解析の設定
解析タイプはNX Nastran ノーマルモード/固有値解析に設定します。
DMIGカードを定義するため、バルクデータオプションの【開始文】にDMIGカード内容を貼り付けします。
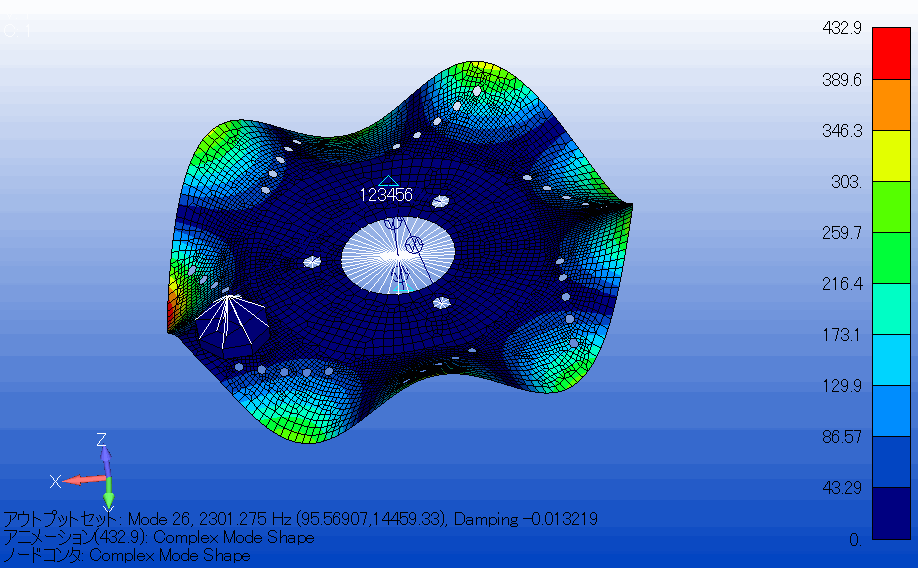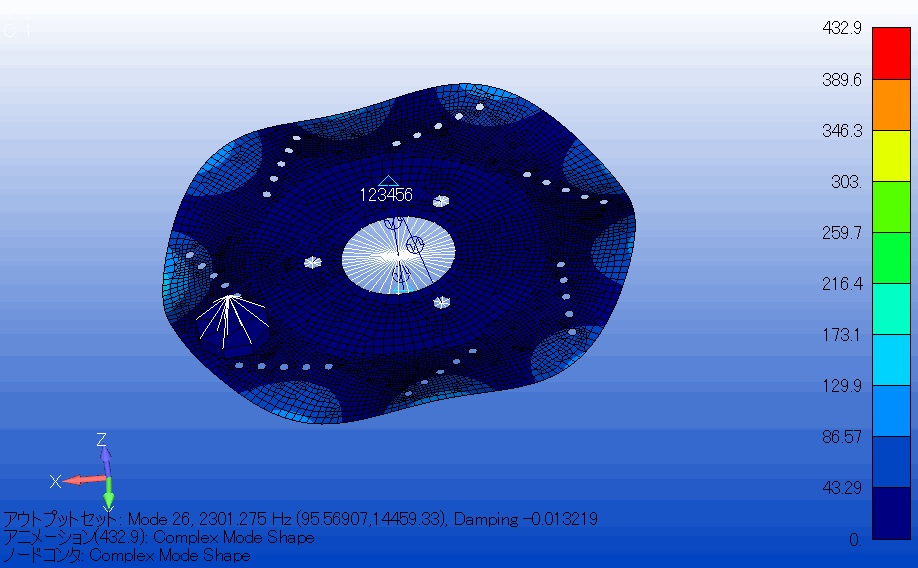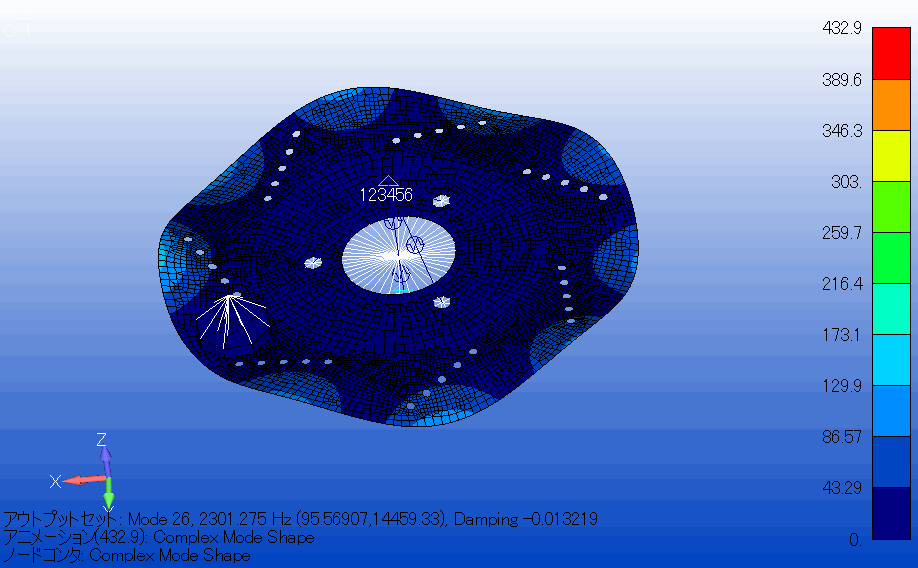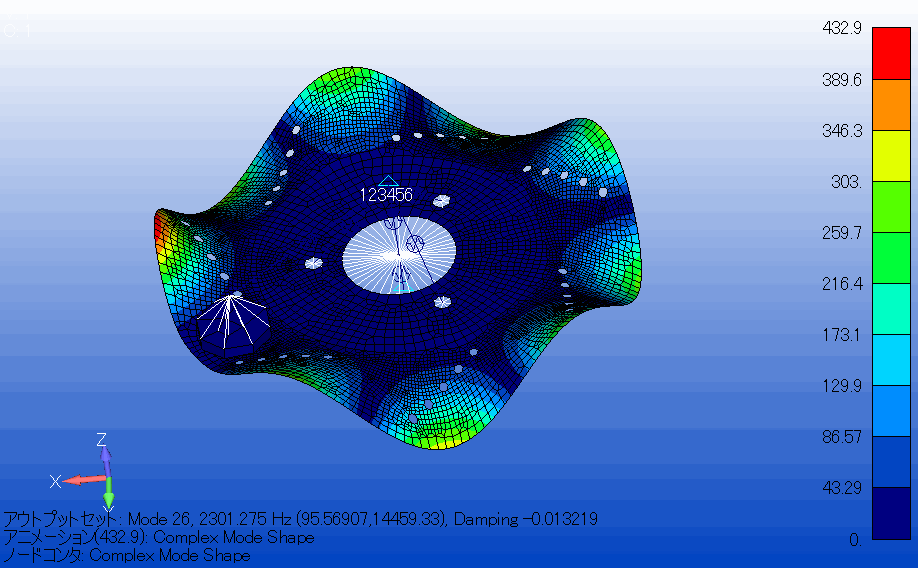
解析結果
解析結果から固有モードの実数部と虚数部のグラフを作成し、モード4(150[Hz]以下の周波数)では、ブレーキの鳴きは発生せず、モード26(2000[Hz]以上の周波数)でブレーキの鳴きが発生することが確認できました。